Понятие оптимальной системы. Синтез и оптимизация параметров

Оглавление

Практически всегда большая система является дорогостоящей, поэтому при ее разработке необходимо спроектировать ее так, чтобы целевой эффект ее применения обеспечивался при минимальных затратах. Возможна также и обратная постановка задачи - проектировать систему так, чтобы вложенные в создание системы ограниченные ресурсы приносили максимальный целевой эффект.

Существует два подхода к проектированию больших систем. Первый и наиболее общий - это синтез. В этом случае формируются самые общие требования к системе, определяется какой должен быть целевой эффект, но сами элементы системы, их функции и связи не задаются. В зависимости от типа системы применятся тот или иной математический аппарат: динамическое программирование Беллмана, метод максимума Понтрягина и др. На этой основе синтезируются элементы системы, их функции и связи, такие что целевой эффект работы системы является максимальным, а требуемые для создания системы ресурсы не превышают заданных. Либо, при обратной постановке задачи, целевой эффект достигает заданного уровня, а затрачиваемые ресурсы минимальны. Метод синтеза хорош тем, что дает глобальный экстремум даже в том случае, если целевая функция носит периодический характер. Графическое пояснение показано на рис.1.

Однако практические задачи с использованием упомянутого математического аппарата решить и довести до уровня реализации удается весьма редко. Поэтому на практике применяют более грубые методы, которые носят название "параметрический синтез" или "оптимизация параметров системы". В отличие от методов прямого синтеза, эти методы не всегда дают глобальный экстремум, однако в рамках задаваемых структуры системы и ее параметров полученные результаты являются приемлемыми для целей практики.

Рассмотрим абстрактный пример. Пусть имеется система, на входе которой действует вектор входных воздействий система имеет параметры 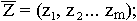выходная целевая функция имеет вид

В данном примере большая система имеет параметры z₁,z₂...z_m и отрабатывает входное воздействие с параметрами x₁,x₂...x_n. Очевидно, что результат функционирования системы, т.е целевая функция зависят как от параметров {z_i} самой системы, так и от параметров входного воздействия {x_i}. Оптимизация параметров системы состоит в том, что при фиксированом (статическом) наборе параметров {x_i} мы можем подбирать параметры системы {z_i} таким образом, что выходная целевая функция R достигает экстремума. Однако, параметры системы должны быть связаны с ресурсными характеристиками, например, со стоимостью. Поскольку изменение каждого из параметров {z_i} системы требует внесения вложения ресурсов: например мы должны увеличить пропускную способность каналов сети или производительность узлов коммутации, а это требует определенных затрат. Поэтому для того чтобы подбор параметров системы был оптимальным, необходимо связать каждый из них с функцией стоимости: z ₁ = f ( d₁ ), z ₂ = f ( d₂ ) и т.д., где d_i i=1,2..m - стоимость изменения параметра. 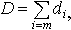В этом случае, изменяя параметры системы z_i, мы будем изменять суммарную стоимость изменения параметров и изменять их таким образом, чтобы стоимость системы была не выше заданной, а целевая функция достигала экстремума. Либо в обратной постановке задачи, мы будем изменять параметры системы так, чтобы ее сумарная стоимость была минимальной, а целевая функция соответствовала заданной.

Метод оптимизации параметров не дает глобального экстремума, по очень простой причине - задавая структуру и состав параметров системы мы уже ограничили свой выбор, и полученный оптимум будет носить частный характер. Однако для решения практических задач этот метод является приемлемым.
 
 

Предыдущий

Следующий