Определение задержки в сети передачи данных
 Оглавление
Оглавление
Определение задержки в сети передачи данных |
 Оглавление
Оглавление
|
Определим величину задержки сообщений в i-х каналах сети и сети в целом. Эти величины будем определять как при известных законах распределения случайных велич T и Ti:
T = Tk + Tобр + Тож
Декомпозируем сеть, выделив из нее один из путей передачи сообщений pij. Он состоит из нескольких узлов и каналов (Рис.1).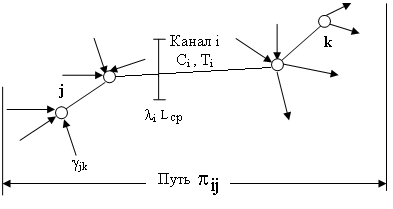
Рис.1
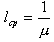 [бит/сообщ].
[бит/сообщ].Определим связь между 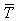 и Ti.
и Ti.
Если 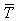 - среднее время задержки в сети,
то среднее число пакетов, находящихся в сети:
- среднее время задержки в сети,
то среднее число пакетов, находящихся в сети:
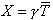 [сообщ],
[сообщ],
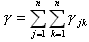 - суммарная интенсивность сообщений,
- суммарная интенсивность сообщений,
С другой стороны, число пакетов, находящихся в очереди к каналу =
liTi, где
li [сообщ/с] - интенсивность на входе каждого канала,
которая определяется процедурой маршрутизации.
Тогда количество сообщений, находящихся в очереди во всех каналах сети:
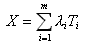 [сообщ]
[сообщ]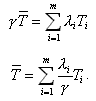
Рассмотрим время обслуживания сообщения в канале Ti. Оно пропорционально длине
сообщения l. В очереди к каналу i находятся сообщения из других линий, а также поступившие в сеть,
т.е. они вышли из разных очередей, поэтому интервалы между поступлениями распределены по сложному закону.
Решить эту задачу можно только представив рассматриваемую систему простейшей M/M/1.
Это означает, что на вход i-той очереди поступает пуассоновский поток сообщений с
интенсивностью li, а время обслуживания распределено по экспоненциальному
закону  .
.
Фактически, это означает, что длина сообщения l выбирается всякий раз новая при поступлении в следующий узел в соответствии с экспоненциальным законом распределения:
Р(l) = mе-ml, l >= 0
Тогда одиночный канал в сети можно представить простейшей одноканальной СМО типа М/М/1. Для такой системы время обслуживания: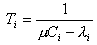 ,
,
Для СПД: m=1/l,
где l - длина сообщения в битах.
Подставляем Ti в выражение для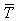 :
:
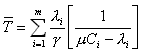 - среднее время сообщений с сети.
- среднее время сообщений с сети.
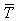 видно, что если знаменатель
mCi - li = 0, то
видно, что если знаменатель
mCi - li = 0, то
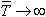 .
.  дает пороговое значение.
дает пороговое значение.Таким образом, 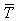 зависит от Сi,
его надо нормировать по стоимости.
зависит от Сi,
его надо нормировать по стоимости.
Для этого будем использовать линейную функцию стоимости:
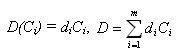
li,
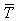 - min,
- min,
Ci - варьируем,
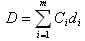 - задано.
- задано.

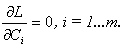
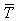 и дифференцируя получим:
и дифференцируя получим:
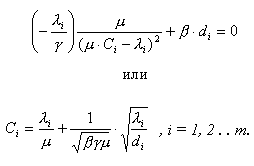
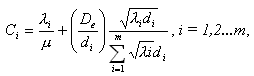 (1)
(1)
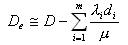 (2)
(2)
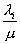 и некоторую добавочную пропускную способность. Это названо распределением Сi пропорционально квадратному корню.
и некоторую добавочную пропускную способность. Это названо распределением Сi пропорционально квадратному корню.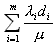 - стоимость минимальной суммарной емкости сети, если De = 0, то
- стоимость минимальной суммарной емкости сети, если De = 0, то
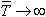 .
.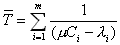 , получим:
, получим:
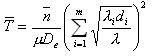 (3)
(3)
 - характеристика топологии сети.
- характеристика топологии сети.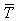 в сети, когда пропускные способности выбраны оптимально.
в сети, когда пропускные способности выбраны оптимально.
Если De > 0 – задача ВПС реализуема, De < 0 – не реализуема.
Для рассмотрения зависимости упростим формулу (1), положив di = d = 1 ( однородная сеть) и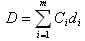 . Тогда
. Тогда
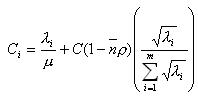
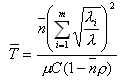
 - коэффициент использования пропускной способности,
- коэффициент использования пропускной способности, .
.
Трафик 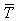 зависит от
зависит от  , значит,
топологию нужно выбирать полносвязную.
Отметим, что равенства получены в предположении, что gjk постоянны.
Если они меняются во времени, то нельзя найти трафик в каналах li и оптимально выбрать Сi,
т.е. сеть не будет оптимальной. Для согласования можно использовать адаптивный выбор
маршрутов, допускающий загрузку недогруженных каналов.
, значит,
топологию нужно выбирать полносвязную.
Отметим, что равенства получены в предположении, что gjk постоянны.
Если они меняются во времени, то нельзя найти трафик в каналах li и оптимально выбрать Сi,
т.е. сеть не будет оптимальной. Для согласования можно использовать адаптивный выбор
маршрутов, допускающий загрузку недогруженных каналов.
 Предыдущий |
 Следующий |