Представление сигналов рядами Фурье |
 Оглавление
Оглавление
|
Для удобства и наглядности дальнейшего анализа воздействия фильтра на сигнал
в частотной области, представим сигнал в виде совокупности элементарных
гармонических сигналов. Гармоническим называют сигнал, описываемый синусоидальной
функцией:
S(t) = Amsin(wt +j), (1)
где Am амплитудное значение сигнала, w
= 2pF - круговая частота, выражаемая в радианах,
F = 1/T - частота сигнала, Т - период следования, j
- начальная фаза сигнала.
Гармонический сигнал характерен тем, что он длится на неограниченном
интервале времени и не может быть разложен на элементарные составляющие.
Известно, что любой сложный периодический сигнал может быть представлен
в виде суммы элементарных гармонических сигналов с помощью рядов Фурье.
Это возможно, если функция, описывающая сигнал, отвечает условиям Дирихле:
-
Функция непрерывна на отрезке разложения;
-
В пределах периода T функция имеет конечное число максимумов и минимумов.
Пусть сигнал описывается функцией S(t), которая имеет частоту w
= 2pF. Применяя разложение в ряд Фурье, получим:
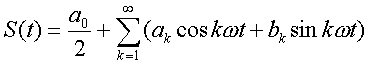 , (2)
, (2)
где k = 1,2.3,... и т.д. - номера гармоник, а амплитуды разложения:
ао, аки bкопределяются из выражений:
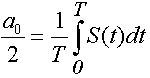 ,
,
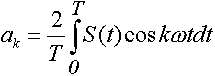 ,
,
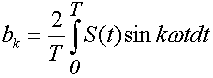 .
.
Понятие спектра
Помимо формы (2) функцию S(t) можно представить в виде:
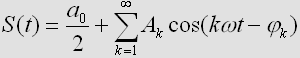 , (3)
где: амплитуда A k и начальная фаза jk определяются из выражений:
, (3)
где: амплитуда A k и начальная фаза jk определяются из выражений:
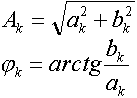 Таким образом, периодическую функцию S(t) можно представить в виде суммы слагаемых, каждое из которых является
синусоидальным колебанием с амплитудой A k и начальной фазой jk.
Таким образом, периодическую функцию S(t) можно представить в виде суммы слагаемых, каждое из которых является
синусоидальным колебанием с амплитудой A k и начальной фазой jk.
Каждая составляющая сигнала с частотой kw называется гармоникой.
Колебание с частотой w называется первой гармоникой, с частотой 2w -
второй гармоникой и т.п.
Совокупность амплитуд гармонических составляющих, представленная как функция частоты называется
амплитудным спектром сигнала (спектром амплитуд). Аналогично, совокупность значений
jk гармоник сигнала, представленная на интервале 0-360 град.,
называется спектром фаз.
Совокупность A k и jk полностью определяют
частотный спектр сигнала.
Спектр амплитуд и спектр фаз для периодического сигнала называют линейчатыми,
так как они состоят из отдельных составляющих. Например, для периодического
сигнала прямоугольной формы, показанного на рис.1,а спектр амплитуд имеет
вид, показанный на рис.1,б.
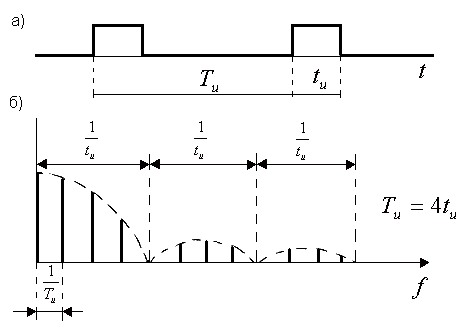
Рис.1
При уменьшении частоты периодического сигнала число гармонических составляющих
в его спектре будет соответственно возрастать, стремясь в пределе к бесконечности.
Такой спектр называется сплошным и получить его можно, используя не ряд,
а интеграл Фурье. Для одиночного прямоугольного импульса
имеем спектр, показанный на рис. 2,б.
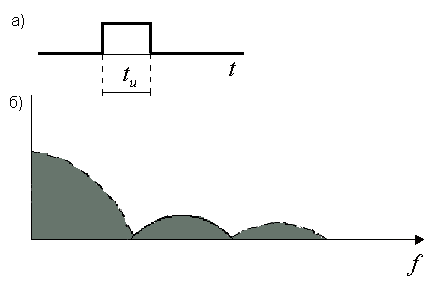
Рис.2
 Предыдущий
Предыдущий
|
|
 Следующий
Следующий
|
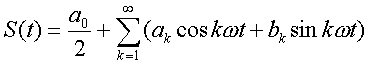 , (2)
, (2)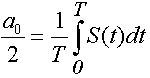 ,
,
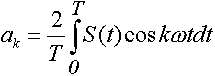 ,
,
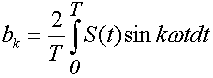 .
.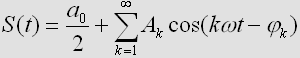 , (3)
, (3)