Представление канала связи в виде 4-х полюсника.

Представление канала связи в виде 4-х полюсника

Оглавление

Для удобства анализа канал представляют в виде 4-х полюсника. Четырехполюсник это абстрактный объект, имеющий две пары зажимов - для входного сигнала и для выходного. Его внутренний алгоритм работы определяется на основании анализа изменений проходящего через него входного сигнала. Процесс прохождения сигнала через канал в теории приема сигналов называют фильтрацией

Рис.1 Схема четырехполюсника

Фильтрация

Процесс прохождения сигнала через канал связи называют фильтрацией. Смысл этого понятия состоит в том, что при прохождении сигнала через канал, часть частот его спектра отфильтровывается и через него не проходит. В теории приема сигналов при анализе свойств канала его принимают линейным инвариантным во времени фильтром. Это означает, что:

Если сигнал s(t) на входе канала порождает выходной сигнал r(t), то для любого t входной сигнал s(t-t) порождает выходной сигнал r(t-t). Это свойство выражает временную инвариантность, а именно если входной сигнал задержан на время t, то соответствующий выходной сигнал остается таким же, за исключением того, что он задерживается на время t.
Если входной сигнал s(t) порождает выходной сигнал r(t), то для любого действительного числа a входной сигнал as(t) порождает выходной сигнал ar(t).
Если входной сигнал s1(t) порождает выходной сигнал r1(t) и входной сигнал s2(t) порождает выходной сигнал r2(t), то сумма входных сигналов s1(t) + s2(t) порождает суммарный выходной сигнал r1(t) + r2(t).
Эти свойства выражают линейность, т.е. если уровень сигнала на входе изменяется в a раз, то соответственно выходной остается таким же по форме, но изменяется по уровню в a раз. Кроме того, выходной сигнал, порожденный суммой двух входных сигналов, равен сумме соответствующих входных сигналов.

При прохождении сигнала через него возникают искажения, обусловленные как характеристиками приемных и передающих устройств, так и внутренними свойствами среды передачи, в которой распространяется сигнал. Одним из следствий фильтрации является сглаживание переданного сигнала s(t). Рассмотрим два примера, в одном из которых s(t) является единичным прямоугольным импульсом, а в другом - последовательностью прямоугольных импульсов.

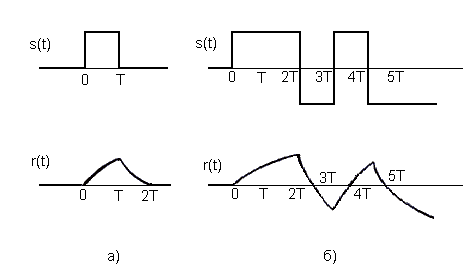
Рис.2

а - отклик r(t) на входной сигнал s(t), являющийся прямоугольным импульсом
б - отклик на последовательность импульсов

Рис.2 Соотношение между входным и выходным сигналами канала связи с фильтрацией.

На рис.2 наглядно показано соответствие между входящими прямоугольными импульсами (битами) и формой аналогового сигнала (биту со значением 1 ставится в соответствие прямоугольный импульс с амплитудой +1, а биту со значением 0 - импульс с амплитудой -1). При увеличении скорости поступления импульсов на вход фильтра, искажения еще более увеличиваются.
На рис.3 показан результат увеличения скорости в 4 раза (т.е. период сигнала уменьшится от Т до Т/4).

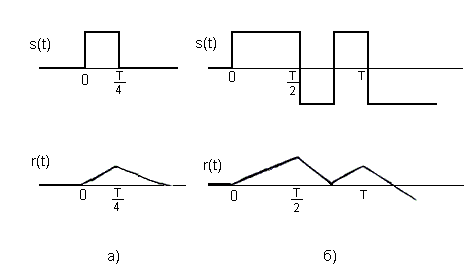
Рис. 3. Соотношение между входным и выходным сигналами при увеличении скорости передачи

На Рис.3.двоичные сигналы поступают в четыре раза быстрее, чем на рис.2 и выходные импульсы становятся в четыре раза короче. Выходной сигнал r(t) в большей степени искажен и ослаблен. Проблема состоит в том, что отклик импульса длится много дольше, чем сам импульс, так что выходной сигнал в заданный момент времени t зависит в значительной степени от полярности нескольких входных импульсов; это явление называется межсимвольной интерференцией.

Интеграл свертки

Выведем математическое соотношение для функции передачи фильтра (канала).
Предположим, что h(t) является сигналом на выходе фильтра , соответствующим бесконечно узкому импульсу единичной площади на его входе , поступающему в момент времени t = 0. Такая функция h(t) называется импульсной характеристикой фильтра (канала). Теперь представим произвольный сигнал s(t) в виде суперпозиции очень узких импульсов шириной d (рис.4).

Рис.4 Графическая интерпретация интеграла свертки.
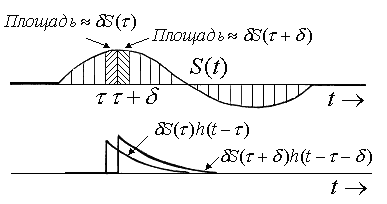
Часть сигнала от s(t) до s(t+d) можно рассматривать как поступивший на вход в момент t узкий импульс площадью ds(t); это приводит к появлению на выходе ds(t)h(t-t) в момент t. Сложение откликов в момент t на каждый из этих входных импульсов и переход к пределу d-->0 показывают, что

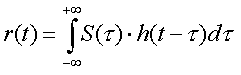(1)

Эта формула называется интегралом свертки, а r(t) называют сверткой s(t) и h(t). Заметим, что из этой формулы следует , что фильтрующие свойства канала полностью определяются импульсной характеристикой h(t). Из этого следует, что при известных импульсной характеристике фильтра и характеристиках сигнала поступающего на его вход, выходной сигнал, являющийся откликом, можно однозначно определить с помощью интеграла свертки.

Передаточная характеристика.

Чтобы получить более полное физическое представление о фильтрации, необходимо наряду с временной областью рассматривать частотную область; другими словами, желательно определить действие фильтрации на синусоиды с различными частотами. Интегрируя (1), получаем
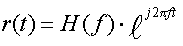(2),
где:
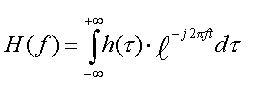(3).
Соотношение (3) отображает произвольную функцию времени h(t) в частотную функцию H(f); математически H(f) является преобразованием Фурье функции h(t). Можно показать, что функцию времени h(t) можно восстановить, зная H(f), с помощью обратного преобразования Фурье

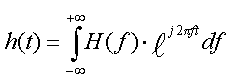(4).

Таким образом, входной сигнал s(t) можно представить (на любом конечном интервале) с помощью частотной функции

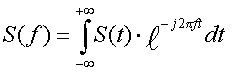(5),

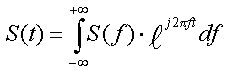(6)

Из линейности канала следует, что отклик на s(t) равен

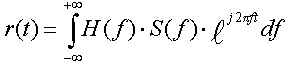(7).

Так как r(t) является обратным преобразованием Фурье R(f), то частотная связь входа и выхода выражается простым равенством

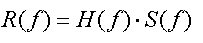(8).

Таким образом, свертке s(t) и h(t) во временной области соответствует умножение H(f) и S(f) в частотной области. H(t) называют передаточной функцией. Из равенства (8) видно, почему спектральный подход способствует пониманию фильтрации. Заметим, что в формуле (8) входной, выходной сигнал и сама передаточная функция являются функциями частоты. В теории связи используется более адекватный термин - амплитудно-частотная характеристика канала.

Предыдущий

Следующий