Понятие связности сети

Оглавление

Одной из важнейших характеристик качества сети является связность. В связном графе для любой пары вершин всегда существует хотя бы одна цепь (маршрут).
Граф можно описать, перечислив все пары узлов, непосредственно соединенных с ним линиями связи. Обычно это делается с помощью целочисленной матрицы, в которой задается число линий от каждого узла ко всем остальным. Эта матрица называется матрицей смежности или матрицей инциденций. При отсутствии петель (циклов), соединяющих узел сам с собой диагональные элементы матрицы равны нулю.

от узла N

	1	2	3	4	5	6
1	х	2	0	0	0	1
2	2	х	1	0	0	0
3	0	1	х	0	0	1
4	0	0	0	х	1	0
5	0	0	0	1	х	0
6	1	0	1	0	0	х

Понятие связности имеет для сети фундаментальное значение. Высокая связность сети предполагает, что такая сеть надежна. Высокая связность, достигаемая при минимальной стоимости сети делает сеть оптимальной.

Существуют детерминированные и вероятностные оценки связности сети.

Детерминированные оценки связности сети

Вершинная (узловая) связность есть мера защищенности графа от распада на не связные части при удалении его вершин.

Удаление узлов 1 и 4 разрывает граф. Вершинная связность k = 2. Удаление ребер, входящих в узел 3 делает граф несвязным Реберная связность графа равна l = 3.

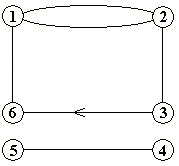
Реберная связность рассматривается как мера защищенности графа сети от распада при удалении из него вершин или ребер. На предыдущем рисунке удаление ребер входящих в узел 3 делает граф несвязным.

Множество узлов, удаление которых делает сеть не связной, также называется узловым сечением. Аналогично, множество ребер, удаление которых делает сеть не связной, называется реберным сечением. Поэтому узловая связность соответствует минимальному узловому сечению, а реберная связность – минимальному реберному сечению. Для проверки связности сети используются матрицы смежности, алгоритмы Форда и Фалкерсона и др.

Вероятностные оценки связности сети

В реальных условиях надежность узлов и каналов связей сети не является абсолютной. Отказы могут происходить вследствие отказов аппаратуры, а также внешних агрессивных воздействий. Поэтому в реальной сети каждый ее компонент, узел или канал, может быть взвешен вероятностью существования. Физически она представляет собой вероятность того, с какой надежностью данный компонент сети выполняет свои функции. В качестве вероятностной меры надежности может быть использована вероятность безотказной работы в течение заданного промежутка времени.

В условиях нарушения работоспособности компонентов сети за счет агрессивных или агрессивных воздействий вероятность связности соответствует живучести сети и используется как мера надежности в сетях военного назначения. Иногда вводят понятие структурной надежности сети, которое эквивалентно понятию надежности.

Наиболее простая характеристика живучести сети – вероятность связности всех вершин графа сети. Состояние сети при удалении части вершин или ребер графа могут быть благоприятными и неблагоприятными. Неблагоприятным состоянием будем считать распад графа на не связанные части с учетом технической надежности и внешних условий работы. Живучесть сети определяется суммой вероятностей всех возможных состояний, в которых вершины графа связаны.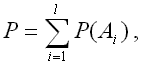

где i = 1, 2,3,…,l
P – вероятность связности всех вершин графа,
А_i – благоприятные состояния, в которых граф оказывается связанным,
P(A_i) – вероятность благоприятного состояния,
l – число благоприятных состояний.

Вероятность связанности сети может быть определена либо методом статистического моделирования сети, либо по формуле:

P_св = P₁P₂P₃...P_m + q₁P₂P₃...P_m + P₁q₂P₃...P_m + ... + P₁P₂P₃...q_m + q₁q₂P₃...P_m + ... + q₁q₂q₃...P_m ,

где P_i – вероятность существования i-го ребра i=1,2,…, m,
q_i = 1-P_i ,
A_i – число возможных соединений i линий в такую цепь, которая обеспечивает связность всех узлов.

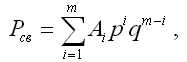
Другой характеристикой надежности сети является вероятность связности 2-х вершин. Две вершины будут связаны тогда, когда в графе существует хотя бы один путь M_i (где i=1…k), связывающий рассматриваемые вершины.
Если B_i – событие, состоящее в том, что хотя бы один такой путь существует, а P(B_i) – вероятность такого события, то вероятность связности 2-хвершин:

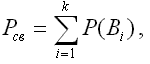
где k- количество цепей или благоприятных случаев).

Для приближенной оценки связности пар узлов используют метод простых сечений. Пару вершин можно рассматривать как фрагмент сети. В некоторых практических случаях требуется определять связность фрагмента сети, включающего от 3 и более узлов в сети. Такой показатель называют фрагментной связностью.

Метод простых сечений удобно рассмотреть на примере: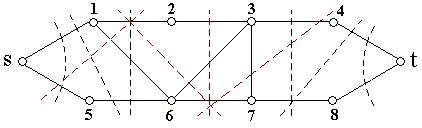

Рис.1

На приведенном рисунке требуется определить связность вершин s и t. Для этого надо определить сечения из 2, 3, 4 и более ребер сети, удаление которых разрывает связь между вершинами s и t. Количество сечений по 2, 3, 4 и т.д. ребер подставляется в формулу:

P_st = ap² + bp² + cp² + ...,

где a, b, c - количество простых сечений по 2, 3, 4 ребра.

В нашем примере разъединение сети произойдет, если выйдет из строя не менее 2-х ребер, таких сечений 6 и 5 сечений по 3 ребра.

Вероятность связности сети оказывает непосредственное вляние на верятностно-временные характеристики доставки сообщений. Из физических соображений ясно, что вероятность доставки сообщений за время не превышающее Тк, неможет превышать вероятности связности сети. Эти два показателя могут быть равны в том гипотетическом случае, если:

каналы первичной сети имеют неограниченную пропускную способность,
узлы коммутации имеют неграниченную производительность,
буферная память узлов коммутации не ограничена.

Предыдущий

Следующий