Помехоустойчивое кодирование.

Помехоустойчивое кодирование

Оглавление

Помехоустойчивые коды

Существенно сократить избыточность в передаваемых сообщения позволяет помехоустойчивое кодирование. В общем плане помехоустойчивое кодирование можно понимать как такое кодирование сообщений, при котором элементы связаны определенной зависимостью, позволяющей при ее нарушении указать ошибки и восстановить информацию. Помехоустойчивые коды рассчитаны на опредеденные ошибки. Это значит, что при других ошибках они могут оказаться недостаточно эффективными.

Принципы помехоустойчивого кодирования

Сообщения по каналу связи передаются в виде кодограммы. Кодограммой, или кодовой комбинацией, называется упорядоченный набор k элементов, каждый из которых может принимать m значений.
Множество всех кодовых комбинаций, поставленных в соответствие сообщениям, называется k-разрядным кодом с основанием m. Таким образом, код - множество кодовых комбинаций, а не одна комбинация.

Пример:

Сообщения	Двоичный код
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001

Коды могут быть:

Безызбыточными - комбинации ставятся в соответствие каким-то сообщениям. В безызбыточном коде искажение любого элемента приводит к перерождению кодовой комбинации, т.е. изменению смыслового содержания сообщения.
Избыточными - использованы не все возможные комбинации. В этих кодах искажение элемента не всегда приводит к искажению сообщения. ( Так, при использовании двоичного кода в случае приема комбинации 1100 неизвестно, какая цифра передана, но и ошибки в распознавании не происходит, так как такой комбинации в коде нет. Ошибка в этом случае обнаруживается. Скорее всего переданы комбинации 1000 или 0100, поскольку они "ближе" к принятой.) Пример избыточного кодирования показан в вышеприведенной таблице.

Идея помехоустойчивого кодирования заключается как раз в таком разнесении кодовых комбинаций, за счет введения избыточности, при котором искажения элементов не приводит к перерождению комбинаций. Разнесение кодовых комбинаций можно изобразить графически.

Сообщениям (число которых не более m^k ) в n-разрядном коде (n = k + r, где r - дополнительные разряды, чтобы код сделать достаточно избыточным) поставили в соответствие такие кодовые комбинации, которые удалены друг от друга максимально. Они образуют корректирующий код. На рисунке кодовые комбинации обведены кружками. Передача этих комбинаций по каналу связи может привести к их искажению. Однако, вероятнее всего они не будут перерождаться в другие кодовые комбинации, а будут переходить в запрещенные для данного кода комбинации, и таким образом ошибки будут обнаруживаться. При достаточно больших расстояниях между кодовыми комбинациями возможно исправление ошибок.

Важнейшие характеристики корректирующих кодов:

корректирующая способность (способность кода к обнаружению и исправлению ошибок);
избыточность.

Корректирующая способность

Избыточные коды иногда называют корректирующими.
Корректирующую способность оценивают минимальным кодовым расстоянием, которое жестко связано с числом исправляемых или обнаруживаемых ошибок. Минимальное кодовое расстояние - это число разрядов, по которым отличаются кодовые комбинации. Обозначается d.

Пример:

10011
11010 ==> кодовое расстояние d=2

Из определения кодового расстояния ясно, что минимальное кодовое расстояние совпадает с минимальным числом одиночных ошибок, приводящих к перерождению кодовых комбинаций корректирующего кода. Поскольку меньшее число ошибок не перерождает комбинацию кода, то корректирующий код позволяет обнаружить d-1 одиночных ошибок.

Если ошибки исправлять по принципу близости полученных кодограмм к кодовым, то можно исправить (d-1)/2 (округляется до целого числа в сторону уменьшения) одиночных ошибок.

Пример: Трехразрядные коды с разными кодовыми расстояниями.

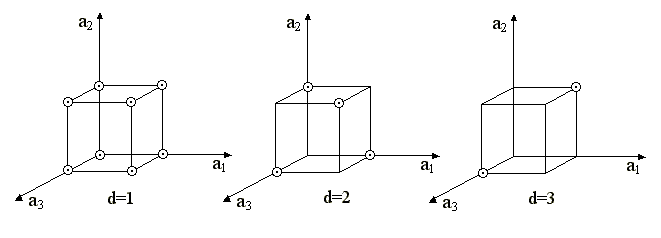
Рис.2

На рис.2 видно, что при d=2 обнаруживается только одиночная ошибка, так как она переводит переданную кодовую комбинацию в разряд запрещенных, и не исправляется ни одной ошибки, что совпадает соответственно со значениями d-1=2-1=1 и (d-1)/2=(2-1)/2=0.

При d=3 одиночные и двойные ошибки переводят кодовые комбинации в запрещенные (они обнаруживаются) , а при одиночной ошибке полученная запрещенная комбинация к переданной кодовой находится ближе, чем к другим (одиночная ошибка исправляется). Тот же результат получается по формулам
d-1=3-1=2 и (d-1)/2=(3-1)/2=1.

Коэффициент избыточности

Количественным показателем избыточности корректирующего кода может служить число, показывающее, во сколько раз уменьшается скорость или увеличивается время передачи сообщений. Коэффициент избыточности определяется отношением:

,
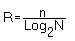где N - число сообщений, n - число разрядов.

Пример: Код с повторением (каждое сообщение повторяется дважды).

Этот код имеет избыточность R=(k+k)/k=2 и минимальное кодовое расстояние d=2, так как обнаруживаются одиночные ошибки и не обнаруживаются двойные ошибки в парных разрядах. Число двойных необнаруживаемых ошибок равно k, и поэтому вероятность необнаружения ошибки (или вероятность перерождения кодовой комбинации) при независимых ошибках приближенно равна

kq²(1 - q)^2k-2 ~ kq²,

где p - веротность появления искажения, а q = 1 - p.

Предыдущий

Следующий
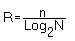